편향 없는 추천 시스템을 위한 통합 학습 전략: 어떻게 숨겨진 변수를 제어할까?

서론

배경

안녕하세요. AI팀 안준형입니다. 오늘은 제가 최근에 봤던 논문 “Removing Hidden Confounding in Recommendation: A Unified Multi-Task Learning Approach” (NeurIPS’23)에 대해서 설명드리려 합니다. 이 논문은 우리가 관측할 수 없는 “숨겨진 혼란 변수”를 제거하여 더욱 공정한 추천시스템 모델을 제시합니다.

서론

추천 시스템은 디지털 환경에서 사용자에게 개인화된 경험을 제공하는 중요한 역할을 수행합니다. 이러한 시스템은 사용자가 과거에 상호작용했던 데이터를 기반으로 추천 모델을 학습시킵니다. 그러나 사용자는 일반적으로 자신의 선호도에 맞는 항목을 선택하는 경향이 있어, 이로 인해 수집된 데이터는 편향될 수 있습니다.

예: 사용자가 특정한 유형의 상품을 선호한다면, 해당 상품에 대한 상호작용이 빈번하게 발생하며 다른 유형의 상품은 상대적으로 드러나지 않게 됩니다. 

이처럼 사용자의 선택적 행동이 반영된 데이터는 전체 데이터와 비교하여 분포가 다를 수 있으며, 이는 추천 모델이 실제 사용자 선호를 제대로 반영하지 못하게 하는 요인이 됩니다. 기존 연구들은 이러한 선택적 편향을 줄이기 위해 다양한 편향 제거 기법을 개발했습니다. 대표적으로는 아래와 같은 방법이 있습니다:

•

오류 보정(error imputation)

•

역확률 가중치(inverse propensity scoring, IPS)

•

이중 강건(doubly robust, DR)

이러한 방법들은 관측된 사용자와 항목의 특성을 활용하여 편향 문제를 보완하지만, 측정되지 않은 숨겨진 혼란 변수(hidden confounding)에는 대응하기 어렵습니다. 숨겨진 혼란 변수란, 사용자와 항목 간 상호작용에 영향을 미치지만 직접 관찰할 수 없는 요인들을 의미합니다.

예: 친구의 추천이나 사용자의 개인적인 환경과 같은 정보는 추천 시스템이 직접적으로 수집하지 못하기 때문에 추천 모델 학습에 영향을 줄 수 있습니다.

본 논문은 기존의 편향 제거 기법들이 숨겨진 혼란 변수를 고려하지 않아 추천 성능에 제한이 발생한다는 문제의식에서 출발합니다. 이를 해결하기 위해, 소수의 편향되지 않은 평가 데이터를 활용하여 숨겨진 혼란 변수의 영향을 최소화하는 새로운 다중 작업 학습 접근법을 제안합니다. 이 방법은 잔차 네트워크(residual networks)를 사용하여 편향된 데이터에서 학습된 명목적 성향(nominal propensity)과 오차를 보정함으로써, 숨겨진 혼란 변수의 영향을 줄이고 보다 공정한 추천 시스템을 구축하는 데 기여할 수 있습니다.

배경

혼란 변수(confounder)의 종류는 아래와 같습니다.

•

관측된 혼란 변수(observed confounder): 현재 feature로 활용되고 있는 데이터.

•

숨겨진 혼란 변수(hidden confounder): 우리가 실제로 관측할 수 없는 데이터.

숨겨진 혼란 변수를 제거하기 위해 기존 인과 추론 연구에서는 도구 변수와 프론트 도어 조정 방식을 제안했으나, 실제 적용에서는 강한 가정이 필요해 검증이 어렵습니다. 최근 연구에서는 민감도 분석을 이용한 '강력한 비혼란 제거 기법(RD)'을 통해 최악의 상황에서도 성향을 제어하려 했지만, 실제 성향이 명목 성향과 일정 범위 내에 있다는 가정이 맞지 않을 경우 한계가 있습니다.

그래서, 이를 완화하기 위해 많은 연구들이 편향되지 않은, 혹은 랜덤 데이터를 사용합니다. 랜덤 데이터는 unbias한 데이터로 gold standard로 여겨지는데, 그 이유는 이러한 데이터는 어떠한 confounder로부터 종속되지(영향받지) 않기 때문입니다. 하지만, 일반적으로 랜덤 데이터의 양이 적기 때문에 이를 가지고만 모델 학습을 하게 된다면 심각한 오버피팅에 빠지게 됩니다. 따라서, 다량의 bias 데이터와 소량의 unbias 데이터를 잘 활용하는 연구들이 많이 존재합니다. 이 논문도 이러한 연구의 일종으로 효과적인 방법을 제시합니다.

방법론

우선 논문에서 정의한 notation은 아래와 같습니다.

Notation	Implication
$\mathcal{D}$	전체 유저, 아이템 pair
$m, n$	유저, 아이템 수
$x_{u,i}$	유저 u 아이템 i의 피쳐
$\mathbf{R} \in \{0,1\}^{m \times n}, \hat{\mathbf{R}} \in \{0,1\}^{m \times n}$	ground truth 전환 매트릭스, 예측값
$r_{u,i}\in \{0,1\}, \hat{r}_{u,i}$	유저 u가 아이템 i에 대한 전환 레이블, 예측값
$o_{u,i} \in \{0,1\}$	유저 u가 아이템 i에 대한 클릭 레이블
$\mathcal{B} = \{(u,i) \| (u,i) \in \mathcal{D}, o_{u,i}=1\}$	클릭 스페이스 (B는 bias를 따온 것)
$\mathcal{U}$	unbias 데이터셋

본 논문에서 제안하는 방법은 잔차 네트워크(residual networks)를 포함한 multi-task learning 방식을 사용하여, 편향된 데이터에서 학습된 명목적 성향(nominal propensity)과 오차를 보정하는 것입니다. 이를 통해 숨겨진 혼란 변수의 영향을 최소화하고, 더 정확한 추천 모델을 학습할 수 있도록 합니다. 이 방법은 편향되지 않은 소수의 데이터를 사용하여 편향된 데이터의 학습 성능을 보완하고, 숨겨진 혼란 변수를 제거하는 데 도움을 줍니다.

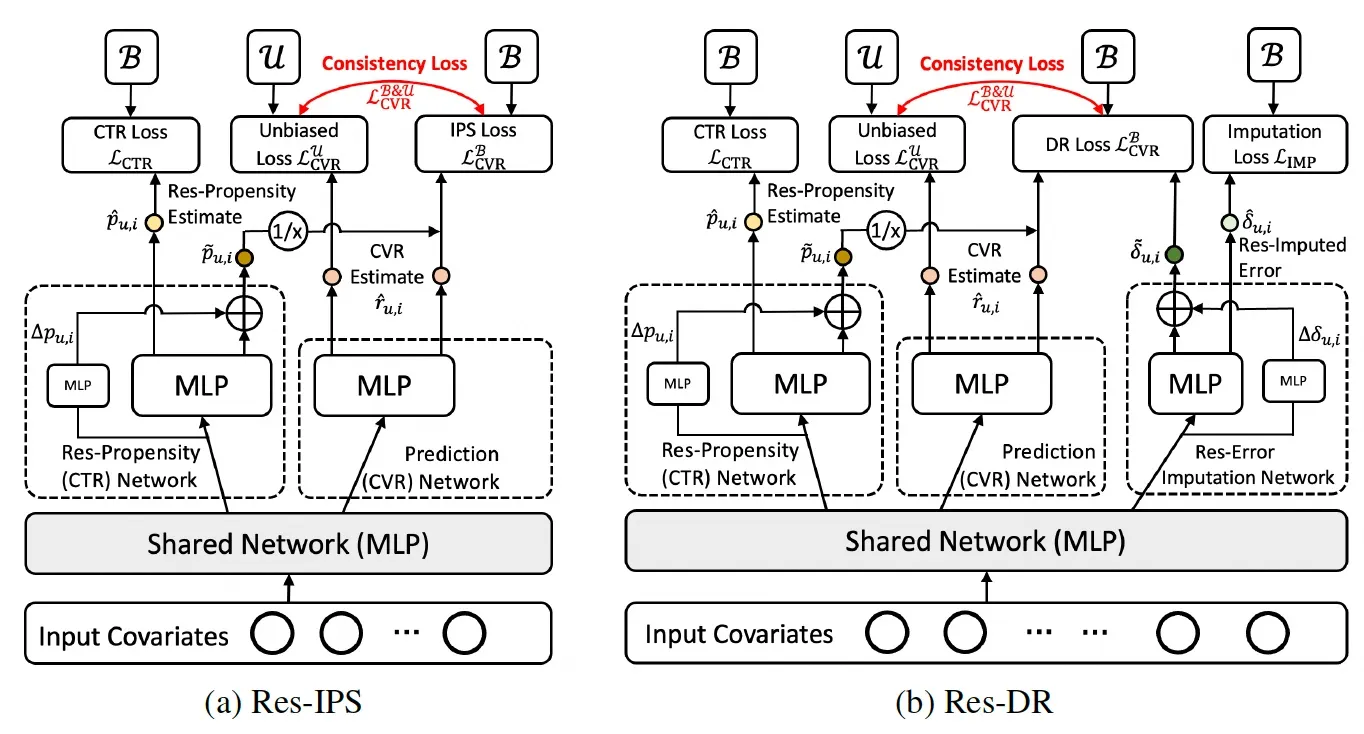
그림 1. 본 논문에서 제시한 메인 모델의 아키텍처

위 그림에서 보면, 잔차 네트워크는 편향된 데이터에서 학습된 성향과 오차를 보정하는 역할을 합니다. 구체적으로, 편향된 데이터에서 학습된 명목적 성향과 오차를 보정하기 위해, 각각의 편향된 데이터에 대해 편향되지 않은 데이터를 활용하여 일관성 손실 함수(consistency loss)를 정의하고, 이를 잔차 네트워크를 통해 학습합니다. 이때, 제안된 접근법은 두 가지 모델을 사용합니다:

•

성향 보정 모델(calibrated propensity model): 편향된 데이터에서 학습된 명목적 성향을 보정하여 실제 성향과 일치하도록 합니다.

•

오차 보정 모델(calibrated imputation model): 편향된 데이터에서 예측된 오차를 보정하여 실제 오차와 일치하도록 합니다.

이러한 잔차 네트워크 기반 보정 모델은 편향된 데이터에서 학습된 성향과 오차를 보정함으로써 숨겨진 혼란 변수를 최소화하고, 전체 모델의 예측 정확성을 향상시킵니다. 또한, 편향되지 않은 데이터에 기반한 일관성 손실 함수를 통해 모델이 숨겨진 혼란 변수를 고려할 수 있도록 학습합니다.

수식으로 한번 살펴보겠습니다. 아래 수식이 이 논문에서 사용하는 최종 손실 함수입니다. Res-IPS와 Res-DR 이렇게 두 모델로 나눠 하나하나 뜯어보겠습니다.

\mathcal{L}_{\text{Res}} = \underbrace{\mathcal{L}_{\text{CTR}}(\hat{p}) + \alpha \cdot \mathcal{L}_{\text{IMP}}(\hat{\delta})}_{\text{Initialization using biased data}} + \beta \cdot \underbrace{\left(\mathcal{L}_{\text{CVR}}^B(\tilde{p}, \tilde{\delta}) + \mathcal{L}_{\text{CTCVR}}^B(\tilde{p}) + \mathcal{L}_{\text{CVR}}^U\right)}_{\text{Prediction model training with calibrated losses}} + \gamma \cdot \underbrace{\mathcal{L}_{\text{CVR}}^{B\&U}(\hat{p}, \tilde{p}, \hat{\delta}, \tilde{\delta})}_{\text{Calibration on } \hat{p} \text{ and } \hat{\delta}}

1) Res-IPS

\mathcal{L}_{Res-IPS} = \mathcal{L}_{CTR} + \alpha_1 \left( \mathcal{L}_{CVR}^{\mathcal{B}} + \mathcal{L}_{CVR}^{\mathcal{U}} \right) + \alpha_2 \mathcal{L}_{CVR}^{\mathcal{B}\; \cup\;\mathcal{U}},

where

\begin{align*} \mathcal{L}_{CTR} &= \frac{1}{|\mathcal{D}|} \sum_{(u,i)\in\mathcal{D}} \delta(o_{u,i}, \hat{p}_{u,i}), \\ \mathcal{L}_{CVR}^{\mathcal{B}} &= \frac{1}{|\mathcal{D}|} \sum_{(u,i)\in\mathcal{D}} \frac{o_{u,i}\cdot \delta_{u,i}}{\tilde{p}_{u,i}}, \\ \mathcal{L}_{CVR}^{\mathcal{U}} &= \frac{1}{|\mathcal{U}|} \sum_{(u,i)\in\mathcal{U}} \delta(r_{u,i}, \hat{r}_{u,i}), \\ \mathcal{L}_{CVR}^{\mathcal{B}\;\cup\;\mathcal{U}} &= \sigma(\mathcal{L}_{CVR}^{\mathcal{B}}, \mathcal{L}_{CVR}^{\mathcal{U}}). \end{align*}

첫 세개의 손실함수는 직관적입니다. 첫번째는 ctr loss, 그리고 2, 3번째는 각각 편향된, 편향되지 않은 데이터에 대한 cvr loss입니다. 편향된 데이터 같은 경우는 편향을 보정해주기 위해 propensity score로 나눠주는 IPS loss를 사용합니다. 반면, 편향되지 않은 데이터는 보정해줄 편향이 없기 때문에 그대로 BCE loss를 사용하는 걸 볼 수 있습니다.

그 다음에 주목해서 봐야할 것은

\mathcal{L}_{CVR}^{\mathcal{B}\;\cup\;\mathcal{U}}

이고, 이 논문에서 제안하는 consistency loss입니다. Consistency loss는 편향되지 않은 데이터를 이용해 편향된 데이터에서 학습된 성향(propensity)과 오차(imputation)를 보정하는 데 중요한 역할을 합니다. 구체적으로, consistency loss는 편향된 데이터셋에서의 IPS (Inverse Propensity Scoring) 또는 DR (Doubly Robust) 추정치와 편향되지 않은 데이터셋에서의 예측 오차 간의 불일치를 최소화하는 방향으로 학습됩니다.

이를 통해 편향된 데이터로 학습한 성향과 오차가 편향되지 않은 데이터의 예측 기준과 일치하도록 보정되며, 이 과정에서 잔차 네트워크가 활용됩니다. consistency loss는 이러한 편향과 불일치를 줄여 모델이 숨겨진 혼란 변수가 존재하는 환경에서도 보다 공정하고 편향 없는 예측을 할 수 있도록 돕습니다. 정리하자면,

•

LCVRU≃Lideal(θCVR)\mathcal{L}_{CVR}^{\mathcal{U}} \simeq 
\mathcal{L}_{ideal}(\theta_{CVR})LCVRU​≃Lideal​(θCVR​)로 여겨집니다.

•

따라서, 편향 손실함수인 LCVRB\mathcal{L}_{CVR}^{\mathcal{B}}LCVRB​와 이상적 손실함수인 LCVRU\mathcal{L}_{CVR}^{\mathcal{U}} LCVRU​의 차이를 loss term에 더해줌으로써, 편향된 데이터를 편향되지 않은 데이터와 비슷하게 동작되도록 만들어줍니다.

2) Res-DR

Res-DR은 오류 보정 손실 함수인

\mathcal{L}_{IMP}

와 ctcvr loss인

\mathcal{L}_{CTCVR}

을 제외하고는 위와 같습니다.

\mathcal{L}_{Res-DR} = \mathcal{L}_{CTR} + \alpha_1 \left( \mathcal{L}_{CVR}^{\mathcal{B}} + \mathcal{L}_{CTCVR}^{\mathcal{B}} + \mathcal{L}_{CVR}^{\mathcal{U}} \right) + \alpha_2 \mathcal{L}_{CVR}^{\mathcal{B}\; \cup\;\mathcal{U}} + \alpha_3\mathcal{L}_{IMP},

where

\begin{align*} \mathcal{L}_{CVR}^{\mathcal{B}} &= \frac{1}{|\mathcal{D}|} \sum_{(u,i)\in\mathcal{D}} \left[ \tilde{\delta}_{u,i} + \frac{o_{u,i}\cdot (\delta_{u,i} - \tilde{\delta}_{u,i})}{\tilde{p}_{u,i}} \right], \\ \mathcal{L}_{IMP} &= \frac{1}{|\mathcal{B}|} \sum_{(u,i) \in \mathcal{B}} \frac{o_{u,i}\cdot (\delta_{u,i} - \hat{\delta}_{u,i})^2}{\hat{p}_{u,i}}. \end{align*}

실험 결과

제안된 방법의 성능을 검증하기 위해 COAT, YAHOO! R3, KUAIREC 세 가지 실제 데이터셋을 사용하여 실험을 수행했습니다. 각 데이터셋에는 편향된 테스트 데이터와 편향되지 않은 테스트 데이터가 포함되어 있어, 다양한 편향 제거 기법의 성능을 평가하기에 적합했습니다.

표 1: 데이터셋 설명

•

YAHOO! R3

◦

311,704 biased ratings

◦

54,000 unbiased ratings

•

COAT

◦

6,960 biased ratings

◦

4,640 unbiased ratings

•

KUAIREC

◦

Industrial dataset

실험에서는 AUC, NDCG@K, Recall@K와 같은 성능 지표를 사용해 제안된 방법의 성능을 평가했습니다.

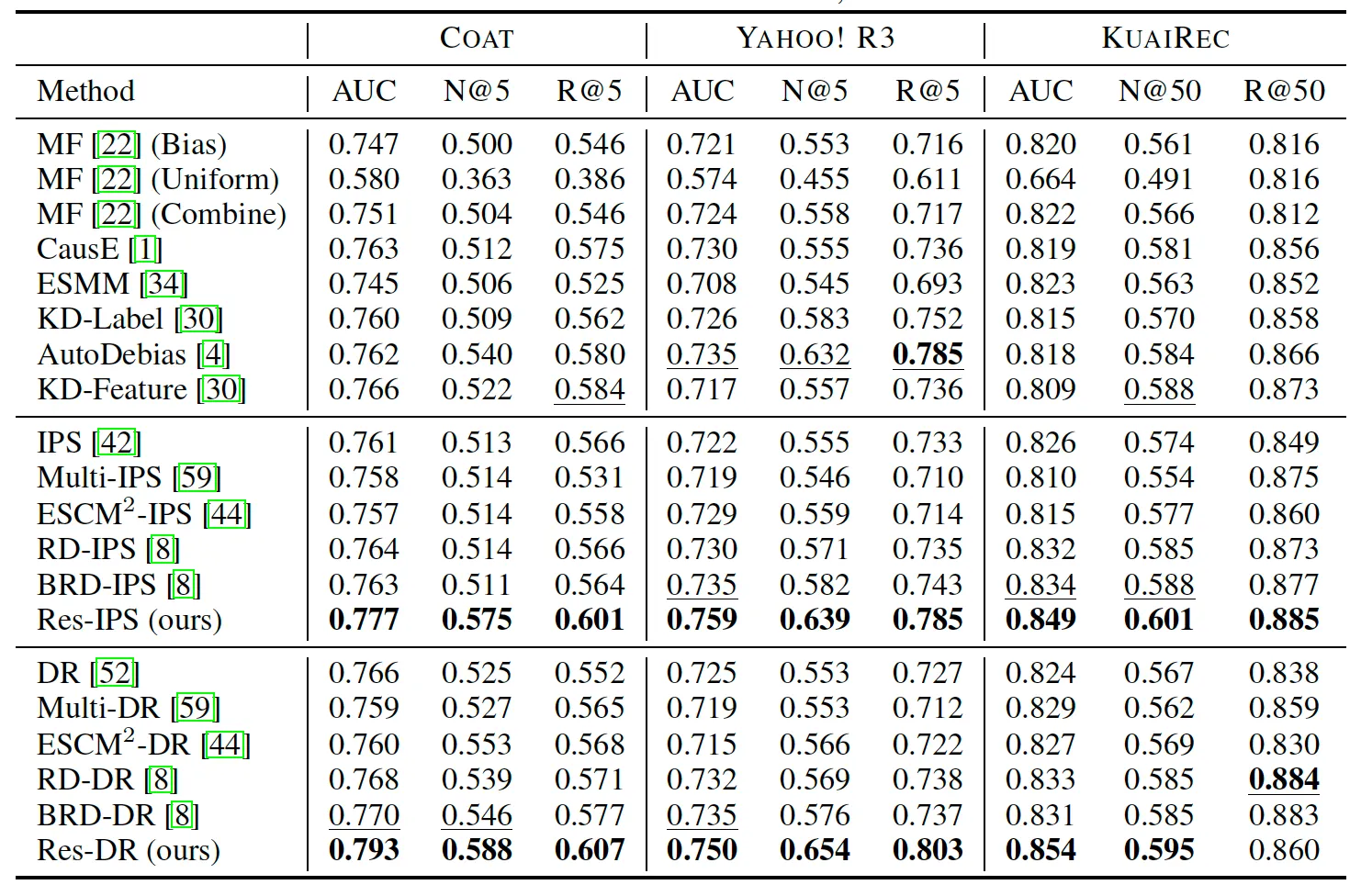
표 2: 다양한 데이터셋에 대한 성능 비교

실험 결과, 제안된 잔차 네트워크 기반 다중 작업 학습 방법(Res-IPS, Res-DR)은 기존의 방법들보다 모든 데이터 세트에서 더 높은 성능을 보였습니다. 특히, 편향된 데이터와 편향되지 않은 데이터를 모두 활용할 때 더욱 탁월한 성능을 나타냈습니다. 예를 들어, COAT 데이터셋에서 Res-IPS는 AUC 0.777, NDCG@5 0.575, Recall@5 0.601을 기록하며, 다른 기존 방법보다 우수한 성능을 보였습니다. 이러한 결과는 숨겨진 혼란 변수가 실제 추천 시스템에 존재함을 시사하며, 본 논문에서 제안하는 방법이 이러한 문제를 해결하는 데 효과적임을 입증합니다.

결론

본 논문은 추천 시스템에서 숨겨진 혼란 변수를 제거하기 위한 새로운 접근 방식을 제안했습니다. 기존의 편향 제거 기법들이 측정된 변수에만 의존하여 숨겨진 혼란 변수를 완전히 해결하지 못하는 한계를 극복하기 위해, 소수의 편향되지 않은 평가 데이터를 통해 학습된 성향과 오차를 보정하는 잔차 네트워크 기반 다중 작업 학습 방법을 소개했습니다.

실험 결과, 제안된 방법은 기존의 편향 제거 기법보다 우수한 성능을 보였으며, 숨겨진 혼란 변수를 최소화하는 데 효과적임을 확인할 수 있었습니다. 특히, 편향되지 않은 데이터와 편향된 데이터를 함께 사용할 때 편향을 더 효과적으로 제거할 수 있음을 알 수 있었습니다. 다만, 본 연구에서는 추가 모델 파라미터가 요구되며, 이는 숨겨진 혼란 변수를 다루기 위한 잔차 네트워크의 필요성에서 비롯된 한계로 남아 있습니다.

이 논문에서 제안된 접근 방식은 추천 시스템의 공정성과 신뢰성을 향상시키는 데 중요한 기여를 할 수 있으며, 향후 데이터 편향 문제를 해결하는 다양한 연구에 중요한 기초가 될 것 같습니다.

참고자료

그림, 표: https://openreview.net/pdf?id=4IWJZjbRFj

작성자

안준형 (Junhyung Ahn)